算法
二叉树的分类
二叉树分为完全二叉树和满二叉树,那么如何区分这2种树呢?
满二叉树:一颗深度为k且有2^k-1个节点的二叉树称为满二叉树;
完全二叉树:在最后一层,并不是所有节点都有两个子节点,这类二叉树又称为完全二叉树
堆
首先来讲一讲堆的结构ba,以下图为例。从根结点开始,每个结点可以有左、右两个结点,元素优先将每一层按从左到右的方式填满,即父结点最多有两个子结点,有右子结点就一定会有左子结点,同一层的某个结点左边一定是填满的。
接下来,说一说堆中元素摆放的规则。堆分为两种情况,有最大堆和最小堆,最小堆就是根结点元素的值是所有元素中最小的,最大堆则相反,下图是一个最小堆。在一个摆放好元素的最小堆中,可以看到,父结点中的元素一定比子结点的元素要小,但对于左右结点的大小则没有规定谁大谁小。
关于最小堆(最大堆)的常用的操作有插入新元素和取最小值(最大值)。
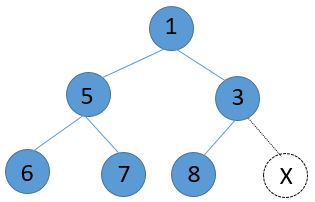
1)插入操作就是直接把新的元素放到最下面一层的可用的最左边,如下图中的X,当X比父结点3要大,那么堆的结构是稳定的,插入操作即完成;如果X比3要小,那么就不符合我们之前说的规则,就要把父结点3和X结点交换,交换完后还没结束,还要比较X和交换完后的父结点即1的大小,如果比1小,则结束,否则仍要继续交换直到稳定。
2)取小值操作,直接将根结点元素返回;此时根结点为空,需要把最后一个叶结点(即结点8)放到根结点的位置,此时把元素8和左右子结点比较小的那一个(即3)作比较,如果比子结点大,则交换,以此累推,直到堆结构稳定。
另外,可以利用堆进行排序,即堆排序,时间复杂度为O(nlogn),具体不在这里讲;关于堆就讲这些简单的知识。
列表(List):
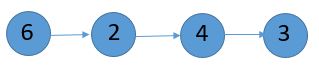
列表是有方向的,如下图所示,结点6是头结点,每个结点除了有相关的元素,还存放指下一个结点的指针,只要知道头指针 head,就可以遍历所有的结点,最后一个结点的指针为空。我们可以定义结点:
struct node{
int value;
struct node next;
};
关于列表的操作有遍历、插入和删除等。
队列(Queue):
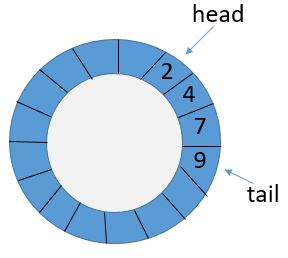
队列可以用一个循环的数组表示,大小为MAX;有头和尾两个标记,插入元素的时候向尾部增加元素,尾标记加1模MAX;删除元素的时候,将头标记加1模MAX;遵循先进先出FIFO原则;
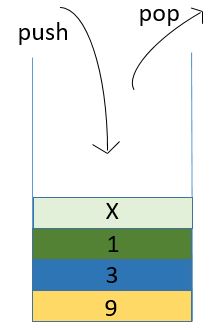
栈(Stack):
与队列相反,栈遵循后进先出LIFO原则;将压入栈的操作称为push,弹出的操作为pop;